Best Fit Lines
In some instances a linear relationship exists between the dependent and independent variables. When a linear relationship exists between the two variables plotted a best fit line can be drawn. The best fit line should pass as close to all of the points as possible but does not necessarily have to pass through any of them. The volume of a liquid sample and its mass are linearly related. In the set of experiments shown below, the volume of a number of liquid samples with different masses were measured, the results were plotted and a best fit line was drawn.
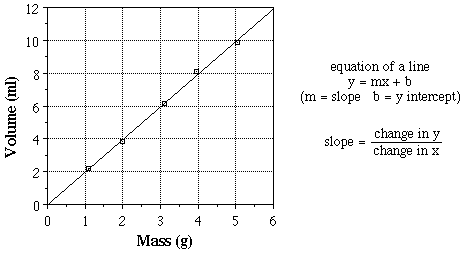
The best fit line can be represented using the equation for a straight line. To determine the slope, determine the slope between two points on the best fit line that lie far apart from each other. Using the points (4.5, 9.0) and (1.5, 3.0) the slope would be (9.0 - 3.0) / (4.5 - 1.5) or 2.0 ml/gram. Reading the y-intercept off this graph (where line crosses the y-axis) gives us a value of -0.1. Therefore, the best fit line has the equation, y = 2.0x - 0.1, or:
volume = 2.0 (mass) - 0.1
The equation of the line could also be calculated using linear regression on a calculator or computer. Performing linear regression on this data gives similar results.
volume = 1.982 (mass) + 0.002
Continue and read about interpolation and extrapolation.









